😗
According to computational complexity theory, mathematical problems have different levels of difficulty in the context of their solvability. While a classical computer can solve some problems ℗ in polynomial time—i.e., the time required for solving P is a polynomial function of the input size—it often fails to solve NP problems that scale exponentially with the problem size and thus cannot be solved in polynomial time. Classical computers based on semiconductor devices are, therefore, inadequate for solving sufficiently large NP problems.
In this regard, quantum computers are considered promising as they can perform a large number of operations in parallel. This, in turn, speeds up the NP problem-solving process. However, many physical implementations are highly sensitive to thermal fluctuations. As a result, quantum computers often demand stringent experimental conditions such extremely low temperatures for their implementation, making their fabrication complicated and expensive.
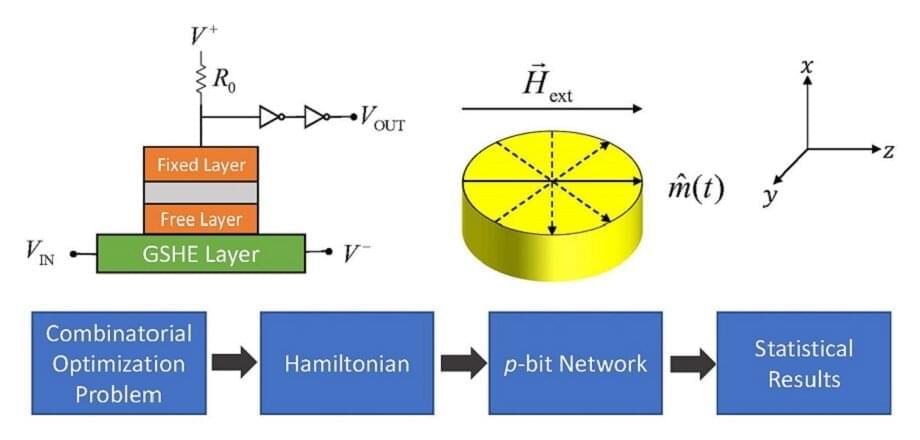
Fortunately, there is a lesser-known and as-yet underexplored alternative to quantum computing, known as probabilistic computing. Probabilistic computing utilizes what are called “stochastic nanodevices,” whose operations rely on thermal fluctuations, to solve NP problems efficiently. Unlike in the case of quantum computers, thermal fluctuations facilitate problem solving in probabilistic computing. As a result, probabilistic computing is, in fact, easier to implement in real life.