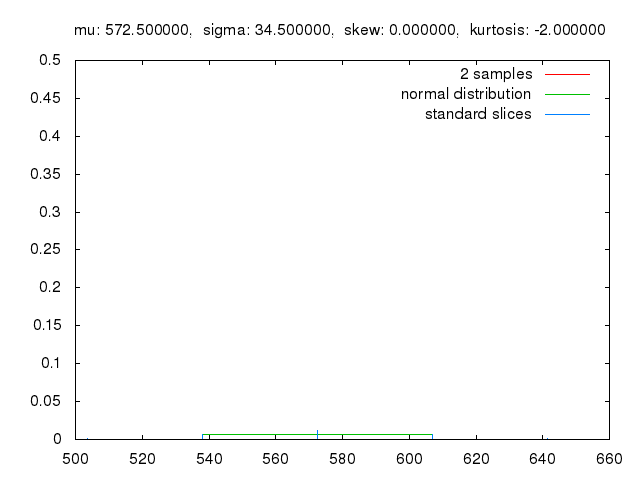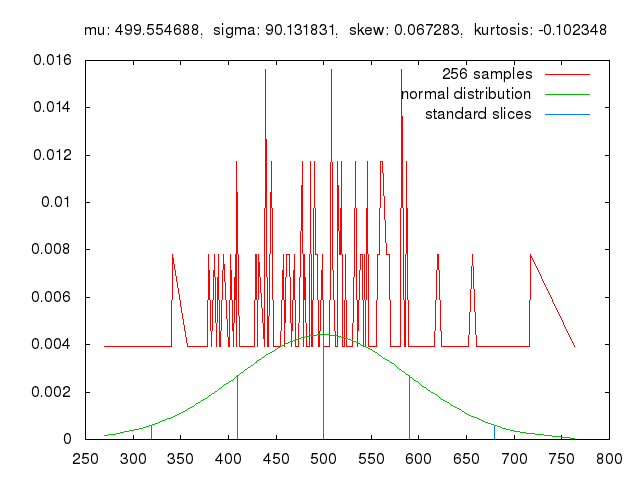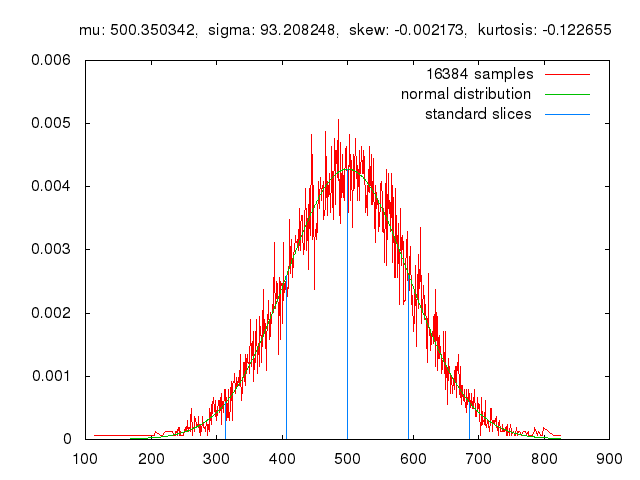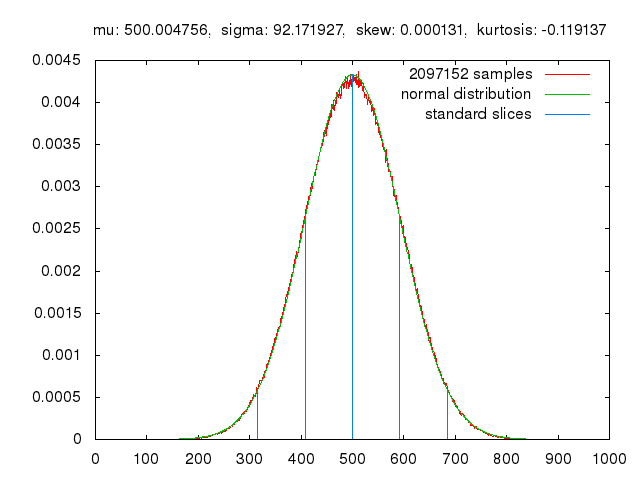Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. The name comes from the Monte Carlo Casino in Monaco, where the primary developer of the method, mathematician Stanisław Ulam, was inspired by his uncle’s gambling habits.
Monte Carlo methods are mainly used in three distinct problem classes: optimization, numerical integration, and generating draws from a probability distribution. They can also be used to model phenomena with significant uncertainty in inputs, such as calculating the risk of a nuclear power plant failure. Monte Carlo methods are often implemented using computer simulations, and they can provide approximate solutions to problems that are otherwise intractable or too complex to analyze mathematically.
Monte Carlo methods are widely used in various fields of science, engineering, and mathematics, such as physics, chemistry, biology, statistics, artificial intelligence, finance, and cryptography. They have also been applied to social sciences, such as sociology, psychology, and political science. Monte Carlo methods have been recognized as one of the most important and influential ideas of the 20th century, and they have enabled many scientific and technological breakthroughs.