High-dimensional spheres can have a much wider variety of structures than mathematicians thought possible.
Category: mathematics – Page 44
Forget politics; if you want to divide a crowd, ask if anyone enjoys mathematics. But even the most maths-averse people may still be impressed by two researchers who have solved a problem that has been stuck in the same puzzling place since 1937.
Julia Eckert, biophysicist at the University of Queensland, recently uncovered nested forms of symmetry in mammalian tissues. This work is bringing the powerful math of fluid dynamics to the messy world of biology.
After identifying interlocking symmetries in mammalian cells, scientists can describe some tissues as liquid crystals — an observation that lays the groundwork for a fluid-dynamic theory of how tissues move.
Dr. Isaac Asimov was a prolific science fiction author, biochemist, and professor. He was best known for his works of science fiction and for his popular science essays. Born in Russia in 1920 and brought to the United States by his family as a young child, he went on to become one of the most influential figures in the world of speculative fiction. He wrote hundreds of books on a variety of topics, but he’s especially remembered for series like the “Foundation” series and the “Robot” series.
Asimov’s science fiction often dealt with themes and ideas that pertained to the future of humanity.
The “Foundation” series for example, introduced the idea of “psychohistory” – a mathematical way of predicting the future based on large population behaviors. While we don’t have psychohistory as described by Asimov, his works did reflect the belief that societies operate on understandable and potentially predictable principles.
Asimov’s “Robot” series introduced the world to the Three Laws of Robotics, which are:
A robot may not injure a human being or, through inaction, allow a human being to come to harm.
A robot must obey the orders given it by human beings, except where such orders would conflict with the First Law.
A robot must protect its own existence as long as such protection does not conflict with the First or Second Law.
These laws have been influential in discussions about robot ethics and the future of AI, even though they are fictional constructs.
Like many futurists and speculative authors, Asimov’s predictions were a mix of hits and misses.
The Nobel Awards Season just ended, with the “Oscars of Science” awarded to some of the world’s brightest minds. The entire science world was watching, and just like with the Oscars, there was an element of suspense, drama, envy, celebration, and happiness. Most of the Nobel Laureates are also phenomenal speakers and communicators with decades of teaching experience, and thousands of people across the world are glued to their monitors to hear their inspiring stories. The Nobel Prizes are awarded in Physics, Chemistry, Physiology or Medicine, Literature, Peace, and Economic Sciences. Unfortunately, there is no Nobel Prize for Computer Science, Mathematics, or Engineering. So, it seems like it… More.
While there is no Nobel Prize for AI, Jumper and Hassabis may be the frontrunners for a Nobel Prize in Chemistry for their discovery of AlphaFold.
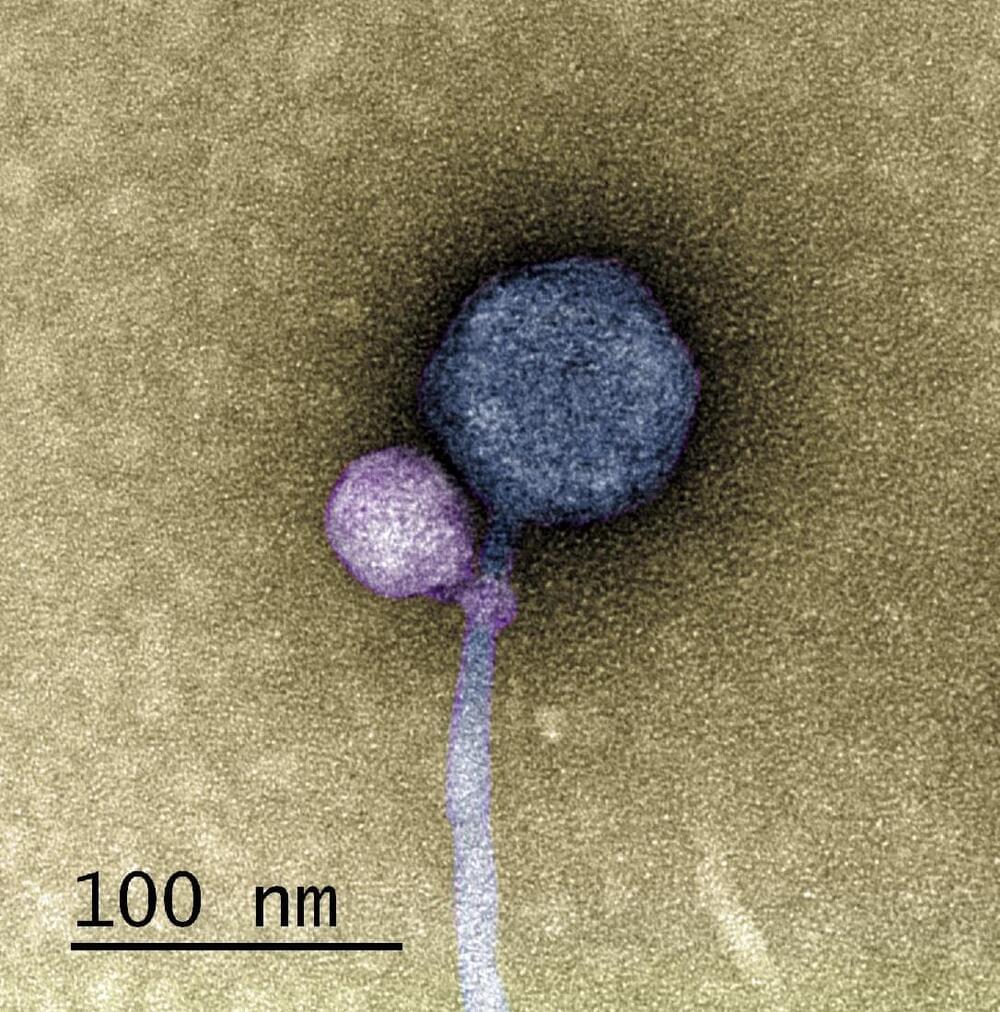
In a paper published in the Journal of the International Society of Microbial Ecology, a UMBC team and colleagues from Washington University in St. Louis (WashU) describe the first observation of a satellite bacteriophage (a virus that infects bacterial cells) consistently attaching to a helper bacteriophage at its “neck”—where the capsid joins the tail of the virus.
In detailed electron microscopy images taken by Tagide deCarvalho, assistant director of the College of Natural and Mathematical Sciences core facilities and first author on the new paper, 80 percent (40 out of 50) helpers had a satellite bound at the neck. Some of those that did not had remnant satellite tendrils present at the neck. Erill, senior author on the paper, describes them as appearing like “bite marks.”
“When I saw it, I was like, ‘I can’t believe this,’” deCarvalho says. “No one has ever seen a bacteriophage—or any other virus—attach to another virus.”
Now, in three papers that together exceed 150 pages, Guàrdia and two collaborators have proved for the first time that instability inevitably arises in a model of planets orbiting a sun.
“The result is really very spectacular,” said Gabriella Pinzari, a mathematical physicist at the University of Padua in Italy. “The authors proved a theorem that is one of the most beautiful theorems that one could prove.” It could also help explain why our solar system looks the way it does.
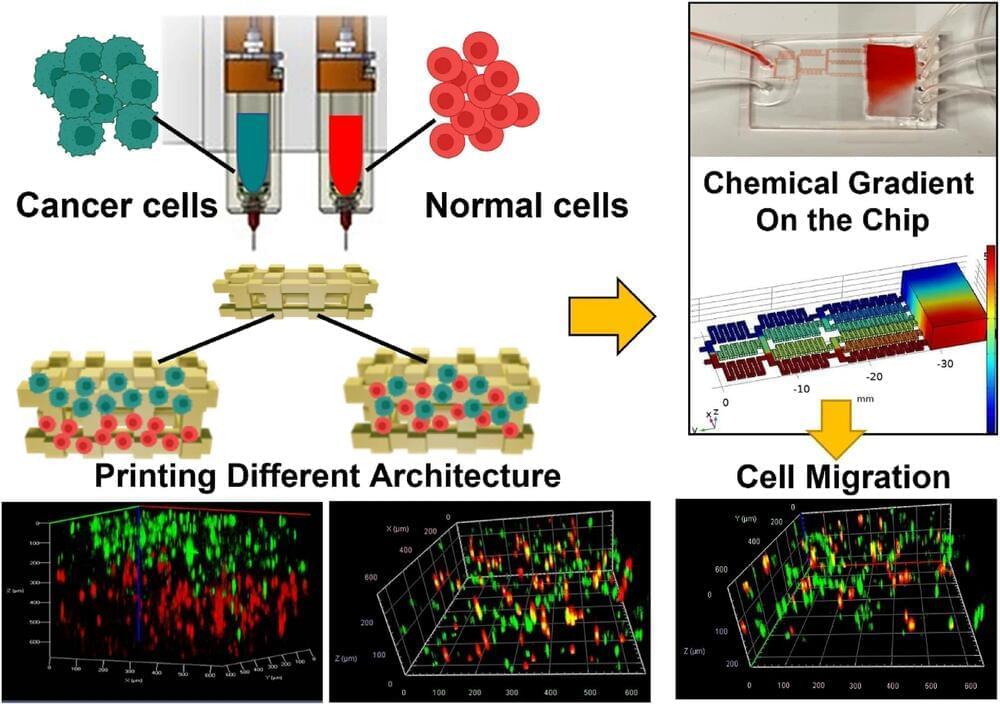
An international team of interdisciplinary researchers has successfully created a method for better 3D modeling of complex cancers. The University of Waterloo-based team combined cutting-edge bioprinting techniques with synthetic structures or microfluidic chips. The method will help lab researchers more accurately understand heterogeneous tumors: tumors with more than one kind of cancer cell, often dispersed in unpredictable patterns.
The research, “Controlled tumor heterogeneity in a co-culture system by 3D bio-printed tumor-on-chip model,” appears in Scientific Reports.
Traditionally, medical practitioners would biopsy a patient’s tumor, extract cells, and then grow them in flat petri dishes in a lab. “For 50 years, this was how biologists understood tumors,” said Nafiseh Moghimi, an applied mathematics post-doctoral researcher and the lead author of the study. “But a decade ago, repeated treatment failures in human trials made scientists realize that a 2D model does not capture the real tumor structure inside the body.”
Möbius strips are fun geometrical shapes that only have one side. Take a strip of paper – it’s got a front and a back. Now twist it and glue the two short edges together. Suddenly there is no front or back. You could draw a line across its whole surface without having to lift the pencil from the paper. Forty-six years ago mathematicians suggested the minimum size for such a strip but they couldn’t prove it. Now, someone finally has.
Since the creation of the strip by August Ferdinand Möbius and Johann Benedict Listing, its simplicity in making and visualizing it had to be balanced with the mathematical complexity of such a shape. It is not surprising that in 1977, Charles Sidney Weaver and Benjamin Rigler Halpern created the Halpern-Weaver Conjecture, which stated the minimal ratio between the width of the strip and its length. They suggested that for a strip with a width of 1 centimeter (0.39 inches), the length had to be at least the square root of 3 centimeters (about 1.73 centimeters or 0.68 inches).
For smooth Möbius strips that are “embedded”, meaning they don’t intersect with each other, the conjecture had no solution. If the strip can go through itself, it is a much easier problem to solve, Brown University’s mathematician Richard Evan Schwartz proposed in 2020 – but he had made a mistake. In a paper posted as a preprint – meaning it is yet to be subjected to peer review – Schwartz corrected the error and found the right solution for the conjecture.
As Shor looked for applications for his quantum period-finding algorithm, he rediscovered a previously known but obscure mathematical theorem: For every number, there exists a periodic function whose periods are related to the number’s prime factors. So if there’s a number you want to factor, you can compute the corresponding function and then solve the problem using period finding — “exactly what quantum computers are so good at,” Regev said.
On a classical computer, this would be an agonizingly slow way to factor a large number — slower even than trying every possible factor. But Shor’s method speeds up the process exponentially, making period finding an ideal way to construct a fast quantum factoring algorithm.
Shor’s algorithm was one of a few key early results that transformed quantum computing from an obscure subfield of theoretical computer science to the juggernaut it is today. But putting the algorithm into practice is a daunting task, because quantum computers are notoriously susceptible to errors: In addition to the qubits required to perform their computations, they need many others doing extra work to keep them from failing. A recent paper by Ekerå and the Google researcher Craig Gidney estimates that using Shor’s algorithm to factor a security-standard 2,048-bit number (about 600 digits long) would require a quantum computer with 20 million qubits. Today’s state-of-the-art machines have at most a few hundred.